The Halton Sequence in MATLAB
This tutorial presents MATLAB code that prices an Asian option using Monte-Carlo simulation in conjunction with the use of the quasi-random Halton sequence. For a general discussion of Monte-Carlo simulation see the Monte-Carlo Methods tutorial. And for a discussion of the mathematical background to Halton's quasi-random sequence see the Variance Reduction tutorial.
Note that the primary purpose of the code presented here is to show how to implement and use the quasi-random Halton sequence to price the option. The code contains no error checking and as such it is not suitable for inclusion into a larger application without appropriate modifications.
MATLAB Function: HaltonSequence
The following MATLAB function gives an example of how to generate the first n numbers in the Halton sequence with base b. A tutorial on the mathematics behind the Halton sequence is also available.
function hs = HaltonSequence(n,b) % Function to generates the first n numbers in Halton's low % discrepancy sequence with base b % % hs = HaltonSequence(n,b) % % Inputs: n - the length of the vector to generate % b - the base of the sequence % % Notes: This code focuses on details of the implementation of the % Halton algorithm. % It does not contain any programatic essentials such as error % checking. % It does not allow for optional/default input arguments. % It is not optimized for memory efficiency or speed. % Author: Phil Goddard (phil@goddardconsulting.ca) % Date: Q2 2006 % Preallocate the output hs = zeros(n,1); % Generate the numbers for idx = 1:n hs(idx) = localHaltonSingleNumber(idx,b); end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Subfunction to generate the nth number in Halton's sequence %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function hn = localHaltonSingleNumber(n,b) % This function generates the n-th number in Halton's low % discrepancy sequence. n0 = n; hn = 0; f = 1/b; while (n0>0) n1 = floor(n0/b); r = n0-n1*b; hn = hn + f*r; f = f/b; n0 = n1; end
MATLAB Function: BoxMuller
The following MATLAB function gives an example of how to generate normal variates from uniform variates using the basic Box-Muller algorithm. The mathematics behind the Box-Muller algorithm are discussed in the Quasi-Random Sequences section of the Monte-Carlo Variance Reduction tutorial.
function sequence = BoxMueller(hs1,hs2) % Function to convert uniform variates into normal variates % using the Box-Muller algorithm. % % sequence = BoxMueller(hs1,hs2) % % Inputs: hs1, hs2 normal sequences (e.g. those generated % by a Halton sequence generator) % % Output: sequence - the normal variate sequence % % Notes: This code focuses on details of the implementation of the % basic Box-Muller algorithm. % It does not contain any programatic essentials such as error % checking. % It is not optimized for memory efficiency or speed, nor is % this particular algorithm the most efficient for performing % the conversion being performed. (It is presented here % for learning purposes as it is relatively easy to understand) % Author: Phil Goddard (phil@goddardconsulting.ca) % Date: Q2 2006 R = sqrt(-2*log(hs1)); Theta = 2*pi*hs2; P = R.*sin(Theta); Q = R.*cos(Theta); sequence = [P;Q];
MATLAB Function: AssetPathsHalton
The following MATLAB function gives an example of how to generate Monte-Carlo sample paths using the HaltonSequence and BoxMuller functions.
function S = AssetPathsHalton(S0,mu,sig,dt,steps,nsims) % Function to generate sample paths for assets assuming geometric % Brownian motion and using Halton's quasi-random sequence. % At each time step a different pair of Halton sequences is % generated using a different pair of prime numbers. % % S = AssetPaths(S0,mu,sig,dt,steps,nsims) % % Inputs: S0 - stock price % : mu - expected return % : sig - volatility % : dt - size of time steps % : steps - number of time steps to calculate % : nsims - number of simulation paths to generate % % Output: S - a matrix where each column represents a simulated % asset price path. % % Notes: This code focuses on details of the implementation of the % Monte-Carlo algorithm. % It does not contain any programatic essentials such as error % checking. % It does not allow for optional/default input arguments. % It is not optimized for memory efficiency or speed. % Author: Phil Goddard % Date: Q2, 2006 % calculate the drift nu = mu - sig*sig/2; % Obtain an 1-by-nsteps vector of prime numbers pVec = primes(1e5); % This will give 9592 numbers bases = pVec(1:2*steps); % generate random samples epsilon = nan(steps,nsims); for idx = 1:steps epsH1 = HaltonSequence(nsims/2,bases(idx)); epsH2 = HaltonSequence(nsims/2,bases(steps+idx)); epsilon(idx,:) = BoxMuller(epsH1,epsH2)'; end % Generate potential paths S = S0*[ones(1,nsims); ... cumprod(exp(nu*dt+sig*sqrt(dt)*epsilon))];
Example Usage
Consider an Asian option with a payoff given by
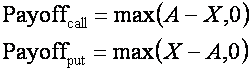
where A is the average price of the underlying asset over the life of the option and X is the strike.
The following code is a MATLAB script that uses the AssetPathsHalton function shown above to generate Monte-Carlo sample paths which are then used to price the option.
% Script to price a Asian option using a Halton sequence S0 =50; % Price of underlying today X = 50; % Strike at expiry mu = 0.04; % expected return sig = 0.1; % expected vol. r = 0.03; % Risk free rate dt = 1/365; % time steps etime = 50; % days to expiry T = dt*etime; % years to expiry nruns = 100000; % Number of simulated paths % Generate potential future asset paths S = AssetPathsHalton(S0,mu,sig,dt,etime,nruns,[2 3]); % calculate the payoff for each path for a Put PutPayoffT = max(X-mean(S),0); % calculate the payoff for each path for a Call CallPayoffT = max(mean(S)-X,0); % discount back putPrice = mean(PutPayoffT)*exp(-r*T) callPrice = mean(CallPayoffT)*exp(-r*T)
The result of executing the above script is,
putPrice =
0.3437
callPrice =
0.4862
An example of pricing the same option using standard Monte-Carlo simulation is available in the Pricing an Asian Option in MATLAB tutorial. Other MATLAB based Monte-Carlo tutorials are linked off the Software Tutorials page.