Generating Correlated Asset Paths in MATLAB
This tutorial presents MATLAB code that generates correlated simulated asset paths as discussed in the Generating Correlated Random Sequences tutorial. The generated paths are suitable to be used in the Monte-Carlo approach to pricing options on a basket of assets. An example of MATLAB code to price a simple Spread option is presented in the Pricing a Spread Option in MATLAB tutorial.
Note that the primary purpose of the code presented here is to show how to efficiently generate the correlated asset paths. The code contains no error checking and as such it is not suitable for inclusion into a larger application without appropriate modifications.
MATLAB Function: AssetPathsCorrelated
The following is code for generating a 3-dimensional matrix where each row represents a time step, each column represent a seperate simulation for a specific asset and the 3rd dimension represents different assets in the basket. The assets are assumed to follow a standard log-normal/geometric Brownian motion model,
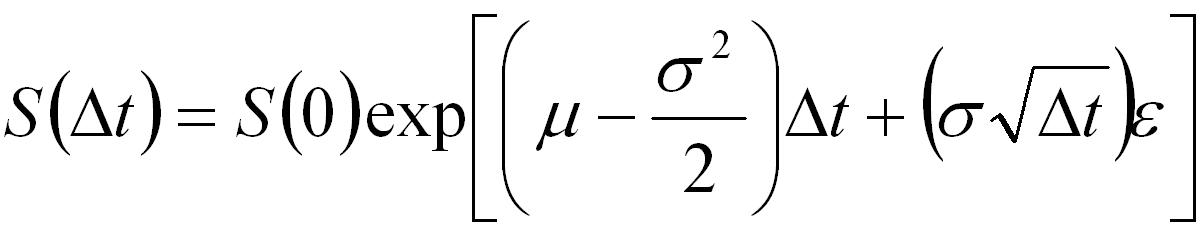
function S = AssetPathsCorrelated(S0,mu,sig,corr,dt,steps,nsims) % Function to generate correlated sample paths for assets assuming % geometric Brownian motion. % % S = AssetPathsCorrelated(S0,mu,sig,corr,dt,steps,nsims) % % Inputs: S0 - stock price % : mu - expected return % : sig - volatility % : corr - correlation matrix % : dt - size of time steps % : steps - number of time steps to calculate % : nsims - number of simulation paths to generate % % Output: S - a (steps+1)-by-nsims-by-nassets 3-dimensional matrix where % each row represents a time step, each column represents a % seperate simulation run and each 3rd dimension represents a % different asset. % % Notes: This code focuses on details of the implementation of the % Monte-Carlo algorithm. % It does not contain any programatic essentials such as error % checking. % It does not allow for optional/default input arguments. % It is not optimized for memory efficiency or speed. % Author: Phil Goddard (phil@goddardconsulting.ca) % Date: Q2, 2006 % get the number of assets nAssets = length(S0); % calculate the drift nu = mu - sig.*sig/2; % do a Cholesky factorization on the correlation matrix R = chol(corr); % pre-allocate the output S = nan(steps+1,nsims,nAssets); % generate correlated random sequences and paths for idx = 1:nsims % generate uncorrelated random sequence x = randn(steps,size(corr,2)); % correlate the sequences ep = x*R; % Generate potential paths S(:,idx,:) = [ones(1,nAssets); ... cumprod(exp(repmat(nu*dt,steps,1)+ep*diag(sig)*sqrt(dt)))]*diag(S0); end % If only one simulation then remove the unitary dimension if nsims==1 S = squeeze(S); end
Example Usage
The following MATLAB code gives an example of how to use the function AssetPathsCorrelated, including creating (and customizing) a plot showing a subset of the generated price paths.
% Script to price an Asian put option using a monte-carlo approach. S0 = [50 48] ; % Price of underlying today mu = [0.03 0.06]; % expected return sig = [0.05 0.1]; % expected vol. corr = [1 0.5;0.5 1]; % correlation matrix dt = 1/365; % time steps etime = 50; % days to expiry T = dt*etime; % years to expiry nruns = 1000; % Number of simulated paths % Generate potential future asset paths S = AssetPathsCorrelated(S0,mu,sig,corr,dt,etime,nruns); % Plot one set of sample paths time = etime:-1:0; plot(time,squeeze(S(:,1,:)),'Linewidth',2); set(gca,'XDir','Reverse','FontWeight','bold','Fontsize',24); xlabel('Time to Expiry','FontWeight','bold','Fontsize',24); ylabel('Asset Price','FontWeight','bold','Fontsize',24); title('One Set of Simulated Asset Paths','FontWeight','bold','Fontsize',24); grid on set(gcf,'Color','w');
The following plot shows one set of correlated asset paths for the given assets,
An example of using the function AssetPathsCorrelated to price a Spread option is presented in the Pricing a Spread Option in MATLAB tutorial.